
请同学们仔细看下面的例子:
Logarithms have important uses in solving problems with complicated exponential equations. Consider the following example:
The population of a small town is 1000 on January 1, 2001. It grows at a constant rate of 2% per year. In what year does the population of the town first exceed 1500?
This question is like the exponential growth problems we’ve just seen but with a twist. Here, we’re given the growth rate, the initial quantity, and the ending quantity. We need to find the number of percent changes (in this case, the number of years) that links all these values. Since logarithms are the power to which you must raise a given number to equal another number, they are the perfect tool for solving this sort of problem.
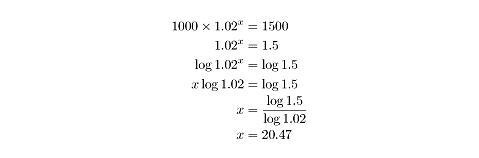
In this case, it will take roughly 20.5 years for the town’s population to exceed 1500. So about halfway through the year 2021, the population will first exceed 1500. The general form for a problem like this one, in which the exponent is unknown, is to isolate the exponential term, take the logarithm of both sides, and then use the power rule of logarithms to bring the variable out of the exponent. You can then isolate the variable on one side of the equation. The base of the logarithms is insignificant. You could choose a base-10 logarithm or a logarithm of any other base, as long as it is consistently used. Here’s a simple example to illustrate this process:
If 6x = 51000, then find the value of x.
This problem would be vastly more difficult if we didn’t have logarithms. How would you possibly calculate 51000 anyhow? And how do you solve for x when it’s the exponent of a number? But by taking the logarithm of each side of the equation, and utilizing the power rule of logarithms:
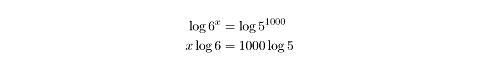
The confusion clears, and we see that we have a logarithm problem that can be methodically solved.

-
SAT数学取得高分的九大答题原则
与SAT其他部分相比,数学部分拿高分对我们中国学生来说并非难事,但同学们不能因此轻视,还是要总结方法争取拿满分,小编分享给大家九大答题原则。希望对考生有所帮助。
- SAT考试数学基础词汇大全
- 新SAT数学首考动向解析
- 新SAT数学考试趋势和难点解析
- SAT数学的难度如何?


